二叉树
先在开头总结一下,二叉树解题的思维模式分两类:
-
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个
traverse函数配合外部变量来实现,这叫**「遍历」**的思维模式。 -
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
-
写递归三步:
- 找整个递归的终止条件:递归应该在什么时候结束?
- 找返回值:应该给上一级返回什么信息?
- 本级递归应该做什么:在这一级递归中,应该完成什么任务?
100. 相同的树
题目
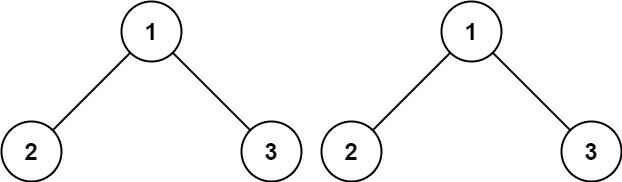
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
思路:
根据函数定义,isSameTree(TreeNode p , TreeNode q)这个函数,输入两个节点,判断以这两个节点为根的子树是否相同
101. 对称二叉树
题目:给你一个二叉树的根节点 root , 检查它是否轴对称。
思路:同上,根据递归函数的定义来求
102. 从根到叶的二进制数之和
思路:
- 这题肯定是需要遍历全部节点得到结果
- 前序遍历,由于是二进制,那么每往下一层,前一层的值就应该乘2,用一个参数记录前面一层的值,遍历到叶子节点就把preSum加到sum中
int sum = 0
public int resolve(TreeNode root){
dfs(root,0);
return sum;
}
public void dfs(TreeNode root,int preSum){
if(root == null){
return;
}
preSum = preSum*2+root.val;//二进制,进入当前层后,要把前面所有层的值都乘二。
//在前序位置判断是否到达叶子节点
if(root.left == null && root.right == null){
sum+=preSum;//如果这步放在后序位置会报错。
}
dfs(root.left,preSum);
dfs(root.right,preSum);
}
110. 平衡二叉树
题目:
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

返回false
思路:
递归计算左右子树的高度,后序位置判断左右子树高度是否相差大于1,如果有一棵子树不平衡,整个二叉树就不平衡
116. 填充每个节点的下一个右侧节点指针
题目
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。

思路:
- 层序遍历
- 递归
递归函数dfs为输入两个节点,并连接它们
public Node connect(Node root) {
dfs(root,null);
return root;
}
public void dfs(Node root, Node next){
if(root == null){
return;
}
root.next = next;
dfs(root.left,root.right);
dfs(root.right,root.next == null ? null:root.next.left);
}
124. 二叉树中的最大路径和【***hard】定义解
题目:
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。路径和 是路径中各节点值的总和。给你一个二叉树的根节点 root ,返回其 最大路径和

思路:
- 分解,用定义
根据题意可以知道,
通过某个节点的最大路径值 = 左子树的最大贡献值 + 右子树的最大贡献值 + 节点值
而某个节点的最大贡献值 = 左右子树的最大贡献值
因为节点有负值,因此,如果该节点的贡献值最小为0,而不是负数。如果节点的某颗子树的贡献值为负数,那么就舍弃它,即将它的贡献值置为0
先写出模版
//函数定义:输入一个根节点,返回这个根节点的贡献值
public int dfs(TreeNode root){
if(root == null){
return 0;
}
int leftGain = dfs(root.left);
int rightGain = dfs(root.right);
//后序位置
return root.val+Math.max(leftGain,rightGain);
}
到了后序位置,通过这个节点的最大路径值就已经得到了,用这个值来更新全局变量,代码变为
public int dfs(TreeNode root){
if(root == null){
return 0;
}
int leftGain = dfs(root.left);
int rightGain = dfs(root.right);
//后序位置
int current = root.val + leftGain + rightGain;//通过当前根节点的最大路径值
maxSum = Math.max(current,maxSum);//更新全局变量
return root.val+Math.max(leftGain,rightGain);
}
543. 二叉树的直径
题目:
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
思路:
-
遍历思路:
- 定义一个递归函数,从父节点遍历至叶子结点
- 定义一个计算最大深度的函数,输入当前节点,输出以当前节点为根的最大深度。
class Solution {
// 记录最大直径的长度
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
// 对每个节点计算直径,求最大直径
traverse(root);
return maxDiameter;
}
// 遍历二叉树
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 对每个节点计算直径
int leftMax = maxDepth(root.left);//以root为根,左子树的最大深度
int rightMax = maxDepth(root.right);//以root为根,右子树的最大深度
int myDiameter = leftMax + rightMax;
// 更新全局最大直径
maxDiameter = Math.max(maxDiameter, myDiameter);
traverse(root.left);
traverse(root.right);
}
// 计算二叉树的最大深度
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
return 1 + Math.max(leftMax, rightMax);
}
}
-
分解思路:
后序遍历,在后序位置判断以当前root为根的子树的直径,与当前所有已经遍历过节点的直径的大小,取最大值更新。
在后序位置,可以获取这个根节点左右子树的最大深度
public int diameterOfBinaryTree(TreeNode root) {
int a = maxDepth(root);
return res;
}
private int maxDepth(TreeNode root){
if(root == null){
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
//在后序位置,可以知道通过root节点的直径为多少
int current = leftMax + rightMax;
res = Math.max(current,res);
return Math.max(leftMax,rightMax)+1;
}
1080. 根到叶路径上的不足节点【定义解】
题目:给定一棵二叉树的根 root,请你考虑它所有 从根到叶的路径:从根到任何叶的路径。(所谓一个叶子节点,就是一个没有子节点的节点)假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit,则该节点被称之为「不足节点」,需要被删除。请你删除所有不足节点,并返回生成的二叉树的根。
思路:
- 分解
先写出函数定义,再根据函数定义来求解。这里要注意定义这个函数的返回值,和在后序位置应该处理的代码逻辑(见代码注释
//函数定义:输入一个根节点,返回这个根节点是否被保留,如果被保留,就返回原始节点,如果不被保留,就返回null。
public TreeNode sufficientSubset(TreeNode root, int limit) {
if(root == null){
return null;
}
if(root.left == null && root.right == null){
//到达叶子结点
return root.val<limit?null:root;
}
root.left = sufficientSubset(root.left,limit-root.val);//limit减小
root.right = sufficientSubset(root.right,limit-root.val);//limit减小
//后序位置,到这里root的左右子树都已经遍历完成了,那么需要判断左右子树是否为空,如果左右子树都空,那么root就需要被删除了,否则保留。
return root.left == null && root.right == null?null:root;
}
- 递归遍历
这里遍历整棵树的时候需要注意,我们可以在根节点上用一个布尔值来决定左右子树是否删除。因此dfs需要返回一个布尔值,如果为 true,就说明应该删除这个节点,反之应该保留。这个布尔值在回溯的时候会在后序位置返回给root节点,从而由root节点来删除它的左右节点
注意,如果我们希望有一个值从root一直往下传递,并在每个节点上都对这个值进行操作,如本题中的preSum。有两种方法
(1)设置一个全局变量,前序位置进行的操作,在后序位置要进行反向操作。比如在前序位置加了,在后序位置就要减
(2)设置为dfs的一个参数,在递归传递参数时,进行操作,比如下面代码
public TreeNode sufficientSubset(TreeNode root, int limit) {
if(root == null){
return null;
}
return dfs(root,0,limit) ? null : root;
}
//函数定义:输入一个root节点,preSum为到这个root节点之前,所有节点的值
private boolean dfs(TreeNode root ,int preSum , int limit){
if(root.left == null && root.right== null){
//到达叶子结点,决定这个叶子节点是否被删除
return preSum+root.val < limit;
}
boolean leftDelete = root.left != null ? dfs(root.left,preSum+root.val,limit) : true;
boolean rightDelete = root.right != null ? dfs(root.right,preSum+root.val,limit) : true;
//后序位置,已经知道左右子树是否被删除了
if(leftDelete){
root.left = null;
}
if(rightDelete){
root.right = null;
}
return leftDelete && rightDelete;
}
1110. 删点成林
题目:
给出二叉树的根节点 root,树上每个节点都有一个不同的值。
如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
思路:
同删除节点,在后序位置判断当前root是否要删除,如果当前root要删除,就添加左右子树。
1367. 二叉树中的链表
题目
如果在二叉树中,存在一条一直向下的路径,且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值,那么请你返回 True ,否则返回 False
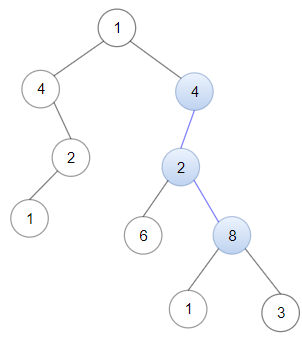
思路
- 写的第一版解法复杂度较高,用的是遍历的思想
boolean flag = false;
public boolean isSubPath(ListNode head, TreeNode root) {
dfs(head,root);
return flag;
}
//遍历每个节点
public void dfs(ListNode head, TreeNode root){
if(root == null){
return;
}
validate(head,root);
dfs(head,root.left);
dfs(head,root.right);
}
//判断以某个节点为根,是否能够成功,如果能成,就修改全局变量
public boolean validate(ListNode head, TreeNode root){
if(head == null){
return true;
}
if(root == null && head != null){
return false;
}
if(root.val == head.val && (validate(head.next,root.left) || validate(head.next,root.right))){
flag = true;
return true;
}
return false;
}
- 第二个题解时间复杂度较低,采用了分解的思路
//一颗树如果满足条件,那么意味着以root节点为根的节点满足条件或root节点的左右子树满足条件
public boolean isSubPath(ListNode head, TreeNode root) {
if(root == null)return false;
return validate(head,root) || isSubPath(head,root.left) || isSubPath(head,root.right);
}
//输入root,判断是否满足条件
public boolean validate(ListNode head, TreeNode root){
if(head == null){
return true;
}
if(root == null){
return false;
}
return root.val == head.val && (validate(head.next,root.left)|| validate(head.next,root.right));
}
1372. 二叉树中的最长交错路径【mid|暴力遍历超时】
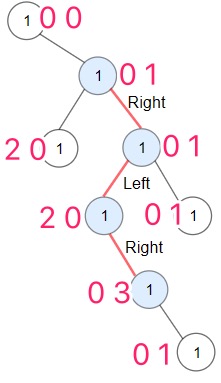
-
从父节点中带两个参数,分别是当前节点作为左孩子的路径长度,和当前节点作为右孩子的路径长度
int path = 0;
public int longestZigZag(TreeNode root) {
if(root == null){return 0;}
dfs(root,0,0);//根节点没有父节点,所以两个都是0
return path;
}
private void dfs(TreeNode root,int l,int r){
if(root == null){
return;
}
path = Math.max(path,Math.max(l,r));
dfs(root.left,r+1,0); //如果往左走,那就把左孩子的l值设为父节点的r+1
dfs(root.right,0,l+1);//如果往右走,那就把右孩子的r值设为父节点的l+1
}
- 暴力遍历,超时
int path = 0;
public int longestZigZag(TreeNode root) {
if(root == null){return 0;}
dfs(root);
return path;
}
private void dfs(TreeNode root){
if(root == null){
return;
}
go(root,true,0);
go(root,false,0);
dfs(root.left);
dfs(root.right);
}
//flag true:左,false:右
private void go(TreeNode root, boolean flag,int level){
if(root ==null){
return;
}
path = Math.max(level,path);
if(flag){
go(root.right,!flag,level+1);
}else{
go(root.left,!flag,level+1);
}
}
修改后:
int path = 0;
public int longestZigZag(TreeNode root) {
if(root == null){return 0;}
dfs(root,true,0); // true说明可以往左走
dfs(root,false,0);
return path;
}
//输入一个root节点
//如果可以往左走,那么就要判断往左走的累加路径和以当前节点为root,往右走的路径
//如果可以往右走,xxxxxx(同上)
private dfs(TreeNode root,boolean dir,int depth){
if(root == null){
return;
}
path = Math.max(depth,path);
if(dir){
//说明可以往左走
if(root.left){dfs(root.left,false,depth+1);}
if(root.right){dfs(root.right,true,1);}//如果往右走了,depth重置为1,因为传到右节点时已经走了一条边
}
}else{
//说明可以往右走
if(root.right){dfs(root.right,true,depth+1);}
if(root.left){dfs(root.left,false,1);}
}
}
二叉树+位运算
222. 完全二叉树的节点个数
题目: 完全二叉树 的根节点 root ,求出该树的节点个数。完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
思路:
-
直接dfs,用一个外部变量记录节点的个数,但是这里不记录这种解法
-
位运算+二分搜索:
完全二叉树的节点路径可以用一个二进制数来表示,比如第二层中有两个节点,它们的索引分别是10,和11,表示第二个和第三个节点。
可以看到这两个数字的最高位都是1,而除最高位外的所有数字表示从根节点到当前节点的路径,0表示左,1表示右。比如10表示第二层,从根节点往左走到达的孩子节点;11表示从根节点往右走到达的节点。
明确了完全二叉树这个性质之后,我们只需要知道它有几层即可。并且对最底层的节点使用二分搜索,最底层的节点索引值范围是:
[1<<height,(1<<(height+1))-1]。表示从根节点一直往左走到达,和从根节点一直往右走到达的节点。二分搜索判断是否存在某一个节点,相当于找一个右边界
代码:
class Solution {
public int countNodes(TreeNode root) {
if(root == null){
return 0;
}
int height = 0;
TreeNode cur = root;
//看这个二叉树有几层。注意,如果有两层的话,这里的height是1。因为第二层的节点,索引有2位,且最高位一定为1。
//因此对于第二层的节点,只需要把1右移1位即可。对于其他层同理。这里的height记录的其实是要右移多少位1。
while(cur.left!=null){
height++;
cur = cur.left;
}
int l = 1<<height;
int r = (1<<(height+1))-1;
//二分找右边界
while(l<=r){
int mid = (l+r)>>1;
if(exist(root,height,mid)){
l = mid+1;
}else{
r = mid-1;
}
}
return r;
}
//validate函数,判断点是否存在
public boolean exist(TreeNode root,int level,int k){
int bit = 1<<(level-1);//要校验的那一位为1,其他为0。校验当前节点要往左还是往右走。比如
TreeNode node = root;
while(node!=null && bit>0){
if((bit & k) == 0){
//如果这一位是0,那么往左走
node = node.left;
} else{
//如果这一位是1,那么往右走
node = node.right;
}
//校验下一位
bit>>=1;
}
return node!=null;
}
}