动态规划

300. 最长递增子序列【重要】

• 题目

  给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

• 思路

这里暴力DP在一些复合困难题中会超时，比如354. 俄罗斯套娃信封问题。因此只记录二分查找法。

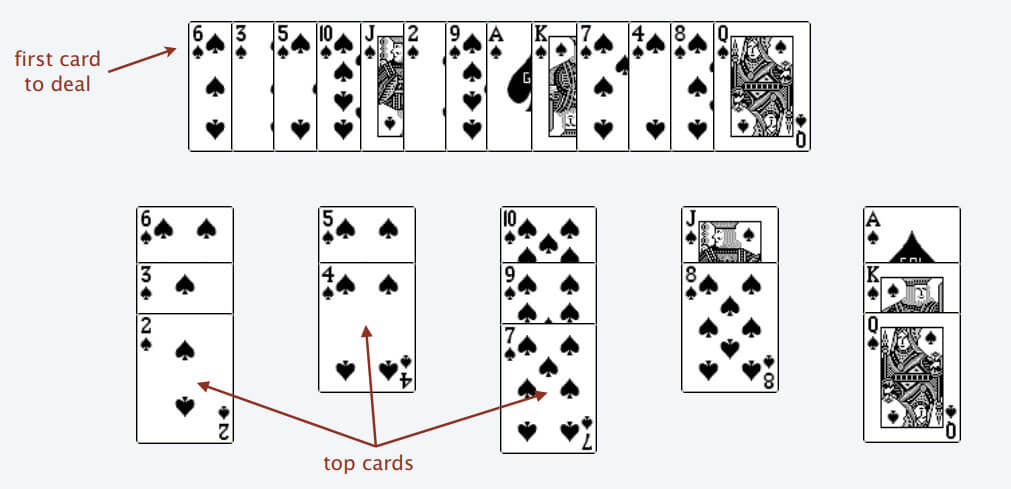
将数组nums按蜘蛛纸牌的方式，放置在不同的牌堆中，**每次放置必须保证这个牌尽可能放在靠前（即左边）的牌堆中。**最后得到的牌堆数就是最长子序列的长度（证明不会）将二分查找法，用在寻找这个数的左边界上，来提速。

二维DP

115. 不同的子序列【重要】

• 题目

  给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

  字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

  eg：s=”bagg“,t=”bag”, return 2，因为s中有2个t的不同子序列。

• 思路

  • 第一步：明确dp的含义。 **做dp的题只需要理解 dp[i][j]的含义是什么，由什么推到出来即可。**在这题中，令 dp[i][j]的含义为 s的前 i个字符，包括第 i个，也就是 s[0...i-1]中有多少个t的前 j个字符。 举个例子，s = “bagg”, t =“bag”，那么 dp[3][3] = 1，因为s的前3个字符”bag”中，有1个t的前三个字符组成的子串” bag”，而 dp[4][3] = 2,因为s的前四个字符”bagg”有2个t的前前三个字符”bag”组成的子串。

  • 第二步：写出状态转移方程：

    $$ dp[i][j] = \begin{cases} dp[i-1][j-1]+dp[i-1][j] , &s[i-1] = t[j-1]\ dp[i-1][j],&s[i-1]!=t[j-1]

    \end{cases} $$

    下面解释一下这个状态方程，当执行到 dp[i][j]时：

    • 当 s[i-1]=t[j-1]时，有两种情况，对应着dp中相加的两项。分别为使用s[i-1]这个字符和不使用s[i-1]这个字符。 如果使用了 s[i-1]那么 dp[i][j]，即子序列数量 = dp[i-1][j-1]，因为当前检测的这两个字符相同，再加上这个字符的子序列数量是等于 s[0....i-2]中 t[0....j-2]的子序列数量的。 如果没有使用 s[i-1]，dp[i][j]，即子序列数量 = dp[i-1][j],说明 s[i-1]这个字符对于子序列数量没有帮助，等于 s[0...i-2]中 t[0···j-1]的子序列数量。
    • 当 s[i-1]!=t[j-1]时，s[i-1]这个字符肯定不能使用，同上，不使用 s[i-1]

    举例：比如s = “bag”,t = “bag”，i = 2,j = 2; s[i-1] = a, t[j-1] = a

    dp[2][2]=dp[1][1]+dp[1][2] ，使用s中的“a”匹配，其子序列数量等于 “b”中 “b” 的子序列数量；不使用s中的”a”进行匹配，其子序列的数量等于”b”中”ba”的数量。

  • 第三步：确定初始状态

    • 初始状态的定义需要根据状态转移方程得出，因为这里矩阵x轴放t，y轴放x。递推从左上方向右下方，上方向下方推进。因此我们要初始化的是第一行和第一列。根据定义得出：
      • 第一行：0 ， 因为代表着 空串中有多少个 t串构成的子序列
      • 第一列：1，代表着 s串中有多少个 空串构成的子序列
      • dp[0][0]：1，代表 空串中有一个 空串构成的子序列

  • 第四步：迭代

    for(int i = 0;i<dp.length;i++){
      for(int j = 0;j<dp[i].length;j++){
        if(s[i-1] == t[j-1]){
          	dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
        }else{
          	dp[i][j] = dp[i-1][j];
        }
      }
      return dp[dp.length-1];
    }
    

• 记忆化搜索写法

class Solution {
    int[][] memo;
    public int numDistinct(String s, String t) {
        int m = s.length();
        int n = t.length();
        memo = new int[m][n];
        for(int i = 0 ;i<m ;i++){
            Arrays.fill(memo[i],-1);
        }
        if(s.length()<t.length()){
            return 0;
        }
        return dfs(s,0,t,0);
    }

    private int dfs(String s , int i ,String t , int j){

        //basecase1: t已经全部匹配完毕，返回1
        if(j==t.length()){
            return 1;
        }
        //basecase2: s剩余的内容长度比t剩余的长度少，t无法匹配完成，返回0。
        if(s.length()-i<t.length()-j){
            return 0;
        }
        if(memo[i][j]!=-1){
            return memo[i][j];
        }
        int res = 0;
        if(s.charAt(i)==t.charAt(j)){
            res = res + dfs(s,i+1,t,j+1) + dfs(s,i+1,t,j);
        }else{
            res += dfs(s,i+1,t,j);
        }
        memo[i][j] = res;
        return res;
    }
}

139. 单词拆分【变式】

• 题目：

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

输入: s = “leetcode”, wordDict = [“leet”, “code”] 输出: true 解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。

• 思路：

  和上一题一样，只不过t变成了单词，而问题变成了s中有没有t组成的子序列。同样按照上面的四步

  • 第一步：dp的含义：

    这道题中，根据问题，dp[i]的含义可以表示为s[0…i-1]是否能够由所提供的单词构成，是一个boolean数组，true表示可以，false表示不可以。

  • 第二步：状态转移方程

    考虑dp[i]怎么由dp[0…i-1]推出。

    如果dp[0…i-1]中有一个位置的值为true，假设这个位置的索引是x，那么我们就需要判断s[x…i-1]，即 s.substring(x,i-1)是否可以组成一个单词，如果可以组成，那么dp[i]就是true，写出状态转移方程。 注：这里dp[i]指的是s[0…i-1]，所以dp[x]=true表示s[0…x-1]可以组成单词，现在需要判断s[x,i-1]是否可以组成单词，所以是 s.substring(x,i)。

    $$ \begin{cases} dp[i] = true,& dp[x]=true&&wordDict.contains(s.substring(x,i)),x\in[0,i-1]\ dp[i] = false, &other \end{cases} $$

  • 第三步：初始化

    这里dp[0]必须为true(这里最后写错了)，不然dp的任何一个值都不可能为true。事实上，dp[0]指的是空串能否被dict中的单词组成。

  • 第四步：迭代

    for(int i = 0;i<dp.length;i++){
      for(int x = 0;x<i;x++){
        dp[i] = dp[i]||(dp[x] && wordDict.contains(s.substring(x,i)));
      }
    }
    return dp[dp.length-1];
    

暴力DP过不了，优化的方法

滑动窗口

模版：

//设置一个双向队列Deque，里面存放nums的索引
Deque<Integer> window = new LinkedList<>();
for(int i = 0 ; i< nums.length; i++){

  //入队过程
  while(!window.isEmpty() && nums[window.pollFirst()]>nums[i]){
    window.pollLast();
  }
  window.offerLast(i);

  //队首元素滑出滑动窗口后的调整过程
  if(i-window.peekFirst()>=k){
    window.pollFirst()
  }

  //一些其他的操作
}

239. 滑动窗口最大值

• 题目：

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7] 解释： 滑动窗口的位置 最大值

---

[1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7

• 思路

设置一个双端队列，Deque<> window = new LinkedList<>()，这个双端队列中队首和队尾都可以出队。这个队列中的元素 w[1],w[2]...w[n]遵循以下规则：nums[w[i]]>nums[w[j]] && w[i]<w[j]也就是说，这个队中存的是nums数组中的索引，且必须保证索引大，值小的数字，排在索引小，值大的数字后面。

举例：比如 nums=[6,1,2,3,8]，window.size=2那么window的变化应该为：

[6]->[6,1]->[6,2]->[6,3]->[8]

为什么这么设定？因为在滑动窗口滑动的过程中，队首元素可能会滑到窗口外，因此我们要选择一个候选人，使得队首元素滑出后，候选人接着成为队首。那么当前在窗口内的元素中，值越大的元素更应该成为候选人，在队中的排列更靠近队首。

明确Deque的定义后，我们要定义队列中的元素什么时候入队什么时候出队。当某个元素可以成为候选人的时候，就入队，当这个元素需要替换队列中的候选人的时候，就while循环，让那些比它差的候选人出队，最后让当前元素入队。

当队首元素滑出滑动窗口了之后，就将队首元素出队，让后面那个候选人当队首元素

• 代码

public int resolve(int[]nums,int k){
  Deque<> window = new LinkedList<>();//注意，这里存的是nums中的索引
	for(int i = 0;i < nums.length ; i++){
    while(!window.isEmpty() && nums[i]<nums[window.peekLast()]){
      //队尾元素不适合当候选人，出队
      window.pollLast();
    }
    //出while以后，向队列中添加新候选人
    window.offerLast(i);

    //判断队首元素是否滑出滑动窗口,如果滑出要更新队首元素
    if(i-window.peekFirst()>=k){
      window.pollFirst();
    }

    //一些其他的操作，本题是将滑动窗口中的最大值加入结果数组中
    if(i>=k-1){
      res[index] = nums[windowIndex.peekFirst()];
      index++;
    }
  }
}

1696. 跳跃游戏 VI

• 题目

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。一开始你在下标 0 处。每一步，你最多可以往前跳 k 步，但你不能跳出数组的边界。也就是说，你可以从下标 i 跳到 [i + 1， min(n - 1, i + k)] 包含 两个端点的任意位置。你的目标是到达数组最后一个位置（下标为 n - 1 ），你的 得分 为经过的所有数字之和。请你返回你能得到的 最大得分 。

输入：nums = [1,-1,-2,4,-7,3], k = 2
输出：7
解释：你可以选择子序列 [1,-1,4,3] 和为 7 。

• 思路，暴力DP的思路如下：

int[] dp = new int[nums.length];
for(int i = 0;i<dp.length;i++){
  for(int j = ; i-j>=0 && j<k ; j++){
    dp[i] = Math.max(dp[j]+nums[i],dp[i]);
  }
}

• 滑动窗口解法：

因为同样的，这里我们只需要找到dp[i-k…i]中的最大值即可，因此用一个滑动窗口来维护这段最大值

状态压缩

一维数组变为两个常量，二维数组变为滚动数组 dp[2][j]

309. 最佳买卖股票时机含冷冻期

题目：

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票。卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

思路：

思路比较简单，直接看代码。注意压缩状态，滚动更新时，存储上一状态的地方

class Solution {
    public int maxProfit(int[] prices) {
        int dp0 = 0;
        int dp1 = Integer.MIN_VALUE;
        int pre0 = 0;
        for(int i = 0 ; i<prices.length;i++){
            int temp = dp0; // 这里存储的是dp[i-1][0],用于更新下面的dp[1]
            dp0 = Math.max(dp0,dp1+prices[i]);
            dp1 = Math.max(dp1,-prices[i]); //前三天可以自由买卖，因为前两天如果买了股票，第1，2天是不可能卖出股票的
            if(i-2>=0){
                dp1 = Math.max(dp1,pre0-prices[i]);
            }
            pre0 = temp; //这里存储的是dp[i-2][0]，用于更新上面的dp[1]。这行代码必须要放在for循环的最后
        }
        return dp0;
    }
}

路径问题【记忆化搜索dfs，dfs转dp，双dp数组】

固定起点，固定方向问题，

可以用一般的二维dp来做，可以优化空间复杂度。

• 滚动数组： 因为下一行的dp值仅与上一行有关，因此，我们只需要开辟 dp[2][n]即可。获取并更新dp值时，用 dp[i &1][j]来更新即可，这等同于 d[i % 2][j]。

• 优先队列： 1289. 下降路径最小和 II

  题目：给你一个 n x n 整数矩阵 arr ，请你返回 非零偏移下降路径 数字和的最小值。非零偏移下降路径 定义为：从 arr 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。 解法：将二维dp数组压缩成一个大小为n的优先队列。每次取头两个元素。分别是上一行中最小的两个值及它们的列索引。当下一行中，列索引与上一行中最小值的列索引相同时，需要用第二小的元素来更新。

记忆化搜索

使用一个memo数组来记录每一次递归的结果，如果有结果直接返回，不会进入dfs

dfs(i){
  if(memo[i]!=-1){
    return memo[i];
  }
}

1575. 统计所有可行路径

题目：

给你一个 互不相同 的整数数组，其中 locations[i] 表示第 i 个城市的位置。同时给你 start，finish 和 fuel 分别表示出发城市、目的地城市和你初始拥有的汽油总量。每一步中，如果你在城市 i ，你可以选择任意一个城市 j ，满足 j != i 且 0 <= j < locations.length ，并移动到城市 j 。从城市 i 移动到 j 消耗的汽油量为 |locations[i] - locations[j]|，|x| 表示 x 的绝对值。 请注意， fuel 任何时刻都 不能 为负，且你 可以 经过任意城市超过一次**（包括 start 和 finish ）**。 请你返回从 start 到 finish 所有可能路径的数目。 由于答案可能很大， 请将它对 10^9 + 7 取余后返回。

思路：

• 记忆化搜索

难点在于定义basecase。做这种题的时候不要多想，直接看dfs的定义，从定义入手。 本题dfs的定义是：dfs(int[] location,int start,int end,int fuel)，代表从 start位置到 end位置，剩余汽油为 fuel的情况下有多少路径数。

public int dfs(int[] location,int start,int end,int fuel){
  int sum = start == end?1:0;//如果start=end，说明当前的路径有一条，就是不用动。
  for(int i = 0;i<location[i];i++{
    if(i!=start){
      //不能自己到自己,不然永远不会跳出循环了。但是可以从end出发，因为题目说可以经过任意城市超过一次
      int need = Math.abs(location[start]-start[i])
      if(need<=fuel){
        //只有汽油足够到，才能计算路径
        sum+=dfs(location,i,end,fuel-need);
        sum%=mod;//题目要求
      }
    }
  }
  memo[start][fuel] = sum; //记录，表示从start开始，到end，剩余汽油为fuel的情况下，有sum条路径
  return sum;
}

优化：

考虑一个baseCase： 如果当前的汽油量无法到达任何一个location，那么就返回0

优化为：如果当前的汽油量无法一步到达终点，那么就返回0

int need = Math.abs(locations[start]-locations[finish]);//如果当前不能一步到达，那么就永远无法到达
if(fuel<need){
  memo[start][fuel] = 0;
  return 0;
}

• dp

  根据记忆化搜索，我们可以将 dfs翻译为状态方程：这里其实dfs的备忘录 memo就是我们的dp数组。dp[i][fuel]表示：从 i出发，剩余汽油 fuel的情况下，到达 finish有多少条路径。

  • 初始状态

    根据记忆化搜索，我们知道初始状态是 dp[finish][fuel] = 1，

  • 状态

    这里的状态是 fuel，和 i。

  • 状态转移方程：f[i][fuel] += f[k][fuel-need]，其中，k是从 i能够到达的地点

代码

for(int i = 0;i<=fuel;i++){
  dp[finish][i] = 1;//初始化路径
}

for(int cur = 0;cur<=fuel;cur++){
 	//最外层fuel
  for(int i = 0;i<n;i++){
    //当前起点i
    if(Math.abs(locations[i]-locations[finish])<0){
      continue;
    }
    for(int k = 0;k<n;k++){
      //i能够到达的k
      if(i!=k){
        int need = Math.abs(locations[i]-locations[k]);
        if(need<=cur){
          dp[i][cur] += dp[k][cur-need];
          dp[i][cur] %= mod;
        }
      }
    }
  }
}

1335. 工作计划的最低难度

题目：

你需要制定一份 d 天的工作计划表。工作之间存在依赖，要想执行第 i 项工作，你必须完成全部 j 项工作（ 0 <= j < i）。你每天 至少 需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和，而一天的工作难度是当天应该完成工作的最大难度。给你一个整数数组 jobDifficulty 和一个整数 d，分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。返回整个工作计划的 最小难度 。如果无法制定工作计划，则返回 -1 。

思路：

【难点】状态转移方程：

dp[i][j] 表示第i+1天，需要完成前j个任务需要的工作难度。
dp[i][j] = dp[i-1][k-1] + max(jobDifficulty[k]到jobDifficulty[n-1])

• 翻译为记忆化搜索：

//dfs(i,j) 表示第i+1天，需要完成前j个任务需要的工作难度。
//dfs(i,j) = dfs(i-1,k-1) + max(k到n-1)
//memo[i][j]表示第i+1天，需要完成前j个任务需要的工作难度，已经计算过了，就不用重复计算了，缩减子问题规模
private int dfs(int day,int job){
  if(memo[day][job]!=-1){
    return memo[day][job];
  }
  if(day==1){
    //只剩一天了，需要返回了
    return max(job);//返回job中的最大值
  }

  int mx = 0;
  int ans = Integer.MAX_VALUE;
  for(int i = job; i>=day; i--){
    mx = Math.max(mx,jobDifficulty[i])
    int ans = dfs(day,i-1) + mx;
  }
  memo[day][job] = ans
  return ans;
}

• 翻译为朴素dp

for (int i = 1; i < d; i++) {
  //天数
  for (int j = n - 1; j >= i; j--) {
    //填充dp[i][...]
    f[i][j] = Integer.MAX_VALUE;
    int mx = 0;
    for (int k = j; k >= i; k--) {
      mx = Math.max(mx, a[k]); // 从 a[k] 到 a[j] 的最大值
      f[i][j] = Math.min(f[i][j], f[i - 1][k - 1] + mx);
    }
  }
}

记忆化搜索分割矩形-华子笔试

1240. 铺瓷砖

题目：

分割一个nxm的矩形，最少需要用到多少块正方形瓷砖

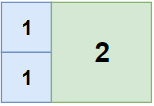
输入：n = 2, m = 3
输出：3
解释：3 块地砖就可以铺满卧室。
     2 块 1x1 地砖
     1 块 2x2 地砖

解答：

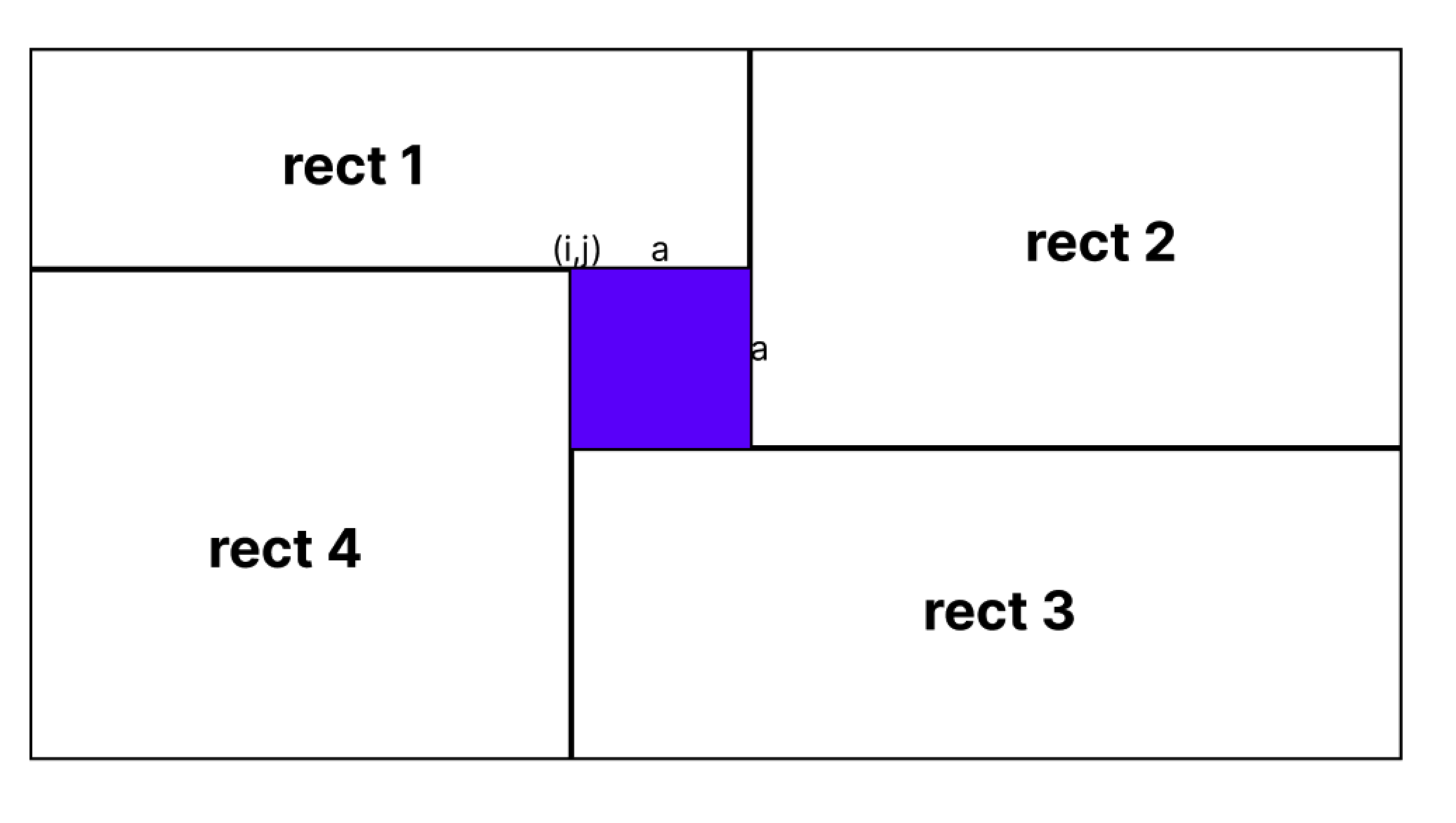
• 设一个大小为a的正方形，放置在 i，j处，将矩形分割为4块：Rect1 ,Rect2, Rect3, Rect4。分割子问题
• dfs(n,m)的定义为：将大小为 n x m矩形使用正方形分割需要用多少块。可以用memo消除重叠子问题

代码

class Solution {
    int[][] memo;
    int cnt;
    public int tilingRectangle(int n, int m) {
        memo = new int[14][14];
        for(int i = 0;i<memo.length;i++){
            Arrays.fill(memo[i],-1);
        }
        return dfs(n,m);
    }

    private int dfs(int n,int m){
        if(n==0||m==0){
            return 0;
        }
        if(memo[n][m]!=-1){
            return memo[n][m];
        }
        int cnt = Math.max(n,m);
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                for(int a=1;a<=Math.min(n-i,m-j);a++){
                    int x1=dfs(i,j+a);
                    int x2=dfs(i+a,m-j-a);
                    int x3=dfs(n-i,j);
                    int x4=dfs(n-(i+a),m-j);
                    cnt=Math.min(cnt,x1+x2+x3+x4+1);
                }
            }
        }
        memo[n][m] = cnt;
        return cnt;
    }
}

统计路径的个数

1301. 最大得分的路径数目

题目：

给你一个正方形字符数组 board ，你从数组最右下方的字符 ‘S’ 出发。你的目标是到达数组最左上角的字符 ‘E’ ，数组剩余的部分为数字字符 1, 2, …, 9 或者障碍 ‘X’。在每一步移动中，你可以向上、向左或者左上方移动，可以移动的前提是到达的格子没有障碍。一条路径的 「得分」 定义为：路径上所有数字的和。请你返回一个列表，包含两个整数：第一个整数是 「得分」 的最大值，第二个整数是得到最大得分的方案数，请把结果对 10^9 + 7 取余。如果没有任何路径可以到达终点，请返回 [0, 0] 。

输入：board = ["E23","2X2","12S"]
输出：[7,1]

思路：

正常dp即可，将”X”字符处的dp值置为 Integer.MIN_VALUE即可。主要是路径数怎么算。

路径数也用dp来做，开一个路径数的dp数组，这里有三个方向:dp[i+1][j+1],dp[i+1][j],dp[i][j+1] ,cnt[m-1][n-1]=1，如果三个方向的dp最大值相同，比如 max = dp[i+1][j+1]=dp[i+1][j] ，那么 cnt[i][j] =cnt[i+1][j+1]+cnt[i+1][j] 。

优化：

因为是正方形，可以把二维dp数组平铺为一维的，加一个转化函数 getIdx(i,j) return i*n+j。

树形DP

题目：

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

eg:

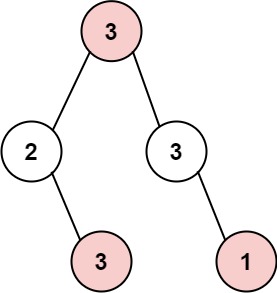
输入: root = [3,2,3,null,3,
null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

思路：

• 分解子问题，使用memo避免重叠子问题

首先明确dfs的定义：dfs(TreeNode root) 表示以root节点为偷窃起点，获取金额的最大值

class Solution {
    Map<TreeNode,Integer> memo = new HashMap<>();
    //定义，返回以当前节点为开始的金额最大值
    public int rob(TreeNode root) {
        if(root == null){
            return 0;
        }
        if(memo.containsKey(root)){
            return memo.get(root);
        }
        int rob = root.val + (root.left == null?0:rob(root.left.left)+rob(root.left.right)) +  (root.right == null?0:rob(root.right.left)+rob(root.right.right));
        int no = rob(root.left)+rob(root.right);
        int res = Math.max(rob,no);
        memo.put(root,res);
        return res;
    }
}

• 【省空间】自顶向下dp，用一个二维数组记录每个节点抢与不抢的最大值金额

dfs返回一个数组，0号位置是抢root，1号位置是不抢root。在后序位置能够获取这个节点的左右子树抢与不抢的最大值。

如果抢root，那么左右子树都不能抢，如果不抢root，那么左右子树抢不抢都行

class Solution {
    public int rob(TreeNode root) {
        return Math.max(dfs(root)[0],dfs(root)[1]);
    }

    private int[] dfs(TreeNode root){
        if(root == null){
            return new int[]{0,0};
        }
        int[] left = dfs(root.left);
        int[] right = dfs(root.right);

        int rob = root.val+left[1] + right[1];
        int no = Math.max(left[0],left[1])+Math.max(right[0],right[1]);
        return new int[]{rob,no};
    }
}

区间DP

1130. 叶值的最小代价生成树

题目：

给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

• 每个节点都有 0 个或是 2 个子节点。
• 数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
• 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。

在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

eg:

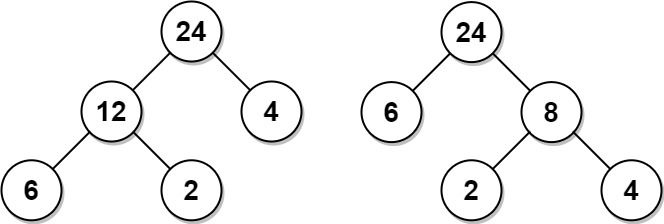
输入：arr = [6,2,4]
输出：32
解释：有两种可能的树，第一种的非叶节点的总和为 36 ，第二种非叶节点的总和为 32 。

思路：

• 确定方法：dp。可以将数组划分为两部分，建树。可以证明任何两个非空子数组都可以建成题目中的树。因此利用数组 arr建成一颗最小代价生成树这个问题可以拆分子问题：将数组拆分成两个子数组，两个子数组都是代价最小的树，那么整棵树代价最小。

• 明确dp含义：dp[i][j]表示当 arr[i]到 arr[j]为叶子结点建成的子树的最小代价。

• 写出状态转移方程：

  $$ dp[i][j] = \begin{cases} 0\ dp[i][j] = dp[i][k] + dp[k+1][j] + mx(i,k) * mx(k+1,j) \end{cases} $$

  其中，mx(i,k)表示 arr[i]到 arr[k]这段子数组中的最大值，最后一项 mx(i,k)*mx(k+1,j)表示根节点的值。

代码：

class Solution {
    public int mctFromLeafValues(int[] arr) {
        int n = arr.length;
        int[][] dp = new int[n][n];
        for(int[] d:dp){
            Arrays.fill(d,Integer.MAX_VALUE);
        }
        int[][] maxval = new int[n][n];
        for(int j = 0;j<n;j++){
            dp[j][j] = 0;
            maxval[j][j] = arr[j];
            for(int i = j-1 ;i>=0; i--){
                maxval[i][j] = Math.max(arr[i],maxval[i+1][j]);//叶子节点的最大值
                for(int k = i; k<j; k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j] + maxval[i][k]*maxval[k+1][j]);
                }
            }
        }
        return dp[0][n-1];
    }
}