双指针数组/链表

双指针：快慢指针的出现是为了将二层循环变为一层。经典题目【删除】

658. 找到 K 个最接近的元素

题目：

给定一个 排序好 的数组 arr ，两个整数 k 和 x ，从数组中找到最靠近 x（两数之差最小）的 k 个数。返回的结果必须要是按升序排好的。

整数 a 比整数 b 更接近 x 需要满足：

|a - x| < |b - x| 或者 |a - x| == |b - x| 且 a < b

思路一：

题意寻找离x最近的k个数，只需要按照它的要求写排序规则即可。排序规则为：与x的差绝对值越小，排位越靠前。最后，用 subList取出前k个数再进行一次排序即可。

思路二：

可以先找到x在数组arr中的位置，即找到两个值，left和right，使得[0,left]的数都小于等于x，[right,arr.lenth-1]的数都大于x。

找位置的问题可以转化为用二分查找找左右边界的问题，这里可以选择找左边界或右边界，找到左边界后，右边界就是left+1；

找到边界后，用两个指针来不断扩大窗口，找到k个数字

80. 删除有序数组中的重复项（通解）

题目：

nums ，请你原地删除重复出现的元素，使得出现次数超过k次的元素只出现k次 （也就是说超出k次的元素要删除），返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

思路一：需要回溯，从后往前，适用于数组，不适用于链表

双指针，一个slow指针用于维护，一个fast指针用于查找。 slow指针之前的元素，即[0,slow)都已经维护完成；fast指针之前的元素，即[0,fast)都已经检查完毕。

因为是有序数组，让出现次数超过k次的元素只出现k次，那么slow的前k个数字arr[slow-k]就不能与当前正在检测的数字arr[fast]相同，如果相同，fast位置的元素就不能保留，如果不相同，那么fast位置的元素就可以保留。

因此，我们需要判断元素是否满足**arr[slow-k]!=arr[fast]，如果 arr[slow-k]==arr[fast]**，那么说明fast指针指向的这个元素不应该被保留，继续检测，如果满足上述条件，那么fast指针指向的这个元素就应该保留，继续检测。

模版

public int removeDuplicatesK(int[] nums,int k){
  int s = k;
  int f = k;
  while(f<nums.length){
    if(nums[s-k]!=nums[f]){
      //保留
      nums[s] = nums[f];
      s++;
    }
    f++;
  }
  return s;//s表示保留几个元素
}

82. 删除排序链表中的重复元素 II

题目：

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

思路：

  • 注意：链表题目如果有可能更改头节点的话，应该设一个虚拟节点dummy，最终返回dummy.next即可

首先，设置一个current节点指向头节点，判断 current.next==current.next.next吗，如果等于的话，我们就需要找到那个不和current.next相等的值，作为current.next

int x = current.next.val;
ListNode node = current.next;
while(node != null && node.next.val==x){
  node = node.next;
}
//退出循环时，node就是我们要接在current后面的节点
current.next = node;

二分搜索【重要】

主要是搜索二分边界的含义

  • 搜索左侧边界的含义。

    • 返回的这个值是 nums 中大于等于 target 的最小元素索引。 比如：【1, 2, 3, 3, 4, 4, 5, 6】target = 3, 返回第一个的索引 2
    • 返回的这个值是 target 应该插入在 nums 中的索引位置。【理解为找到一个区间】 比如：【1, 4, 6, 8, 10】,target = 2，返回应该插入的索引 1。
    • 返回的这个值是 nums 中小于 target 的元素个数。 同上，比如【1, 4, 6, 8, 10】,target = 4，返回个数 1。target = 7，返回个数 3。

  • 搜索右侧边界的含义

二分搜索答案空间

一般都是暴力会超时，用二分提速。

1011. 在 D 天内送达包裹的能力

题目：

传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量（weights）的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。

输入：weights = [1,2,3,4,5,6,7,8,9,10], days = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10

思路：

由于枚举答案空间会超时，因此在答案空间中用二分搜索找答案。答案空间：[max(weight),sum(weight)]，找满足运输条件的左边界。

public int shipWithinDays(int[] weights, int days) {
  //设定左右边界
  int sum = 0;
  int max = 0;
  for(int w:weights){
    sum+=w;
    max = Math.max(max,w);
  }
  int l = max;
  int r = sum;

  while(l<=r){
    int mid = l+((r-l)>>1);
    if(validate(mid,weights,days)){
      //validate用来判断能否完成运输
      r = mid-1;
    }else{
      l = mid+1;
    }
  }
  return l;
}
410. 分割数组的最大值

题目：

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

思路：

这题的难点有三个：

  • 找到二分空间
  • 找到m与最大值的关系
  • 找到二分查找的条件

下面一个一个来解决。

第一步：找到二分空间，子数组最大值的取值范围应该是 [数组中的最小值，数组的和]

第二步：找到m与最大值的关系，从二分空间中可以看出，如果子数组的最大值取数组中的最小值，那么数组会被分割成 n=nums.length个；如果子数组的最大值取数组的和，那么数组会被分割成 1个。

第三步：从第二步可以看出，子数组的最大值取的越大，被分割的个数就越大；反之，子数组的最大值取的越小，被分割的个数就越少。因此我们可以找到这个值的左边界，使得满足子数组被分割的个数=m。

2517. 礼盒的最大甜蜜度

题目：

给你一个正整数数组 price ，其中 price[i] 表示第 i 类糖果的价格，另给你一个正整数 k 。商店组合 k 类 不同 糖果打包成礼盒出售。礼盒的 甜蜜度 是礼盒中任意两种糖果 价格 绝对差的最小值。返回礼盒的 最大 甜蜜度。

输入：price = [13,5,1,8,21,2], k = 3
输出：8
解释：选出价格分别为 [13,5,21] 的三类糖果。
礼盒的甜蜜度为 min(|13 - 5|, |13 - 21|, |5 - 21|) = min(8, 8, 16) = 8 。
可以证明能够取得的最大甜蜜度就是 8 。

思路：

非常重要的一点：最小的最大，最大的最小，基本都是二分

因为最小的最大代表寻找右边界，最大的最小代表寻找左边界

知道使用二分以后，代码其实就很好写了。因为题目需要寻找最大的甜蜜度，因此我们需要二分甜蜜度，而二分的判断条件就用当前甜蜜度可以装入多少种糖果来作为条件。假设在 t甜蜜度下，可以放入 cnt种糖果，且 cnt>=k，那么说明甜蜜度还可以更大，让 cnt更小，此时我们就要继续向右寻找，据此可以写出如下二分代码

class Solution {
    public int maximumTastiness(int[] price, int k) {
        //找右边界
        Arrays.sort(price);
        int max = -1;
        int n = price.length;
        int l = 0;
        int r = price[n-1]-price[0];
        while(l<=r){
            int mid = (l+r)>>1;
            if(validate(price,k,mid)){
                l = mid+1;
            }else{
                r = mid-1;
            }
        }
        return r;
    }
    private boolean validate(int[] price, int k,int t){
        int prev = price[0];
        int cnt = 1;
        for(int p:price){
            if(p-prev>=t){
                cnt++;
                prev = p;
            }
        }
        //如果有很多都满足，那么我可以让甜蜜度更大一些
        return cnt>=k;
    }
}

递归链表题【不太掌握】

涉及到反转的问题，都可以化整为零，及讲一个复杂的反转问题，转化到基础的化简问题上来

反转整个

206. 反转链表

题目：

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

思路；

模版：注意basecase，dfs的 return值，和修改逻辑

可以修改前驱节点

class Solution {
    public ListNode reverseList(ListNode head) {
        return dfs(head);
    }

    private ListNode dfs(ListNode head){
        if(head == null || head.next == null){
            return head; //到最后一个节点返回
        }
        ListNode node = dfs(head.next);
        head.next.next = head;
        head.next = null; // 前驱节点
        return node; // node一直指向最后一个节点
    }
}

反转前N

代码：

private ListNode reverseN(ListNode head, int n){
    if(n==1){
        pre = head.next;
        return head;
    }
    ListNode last = reverseN(head.next,n-1);
    head.next.next = head;
    head.next = pre;
    return last;
}

反转区间

92. 反转链表 II

题目：

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

思路：

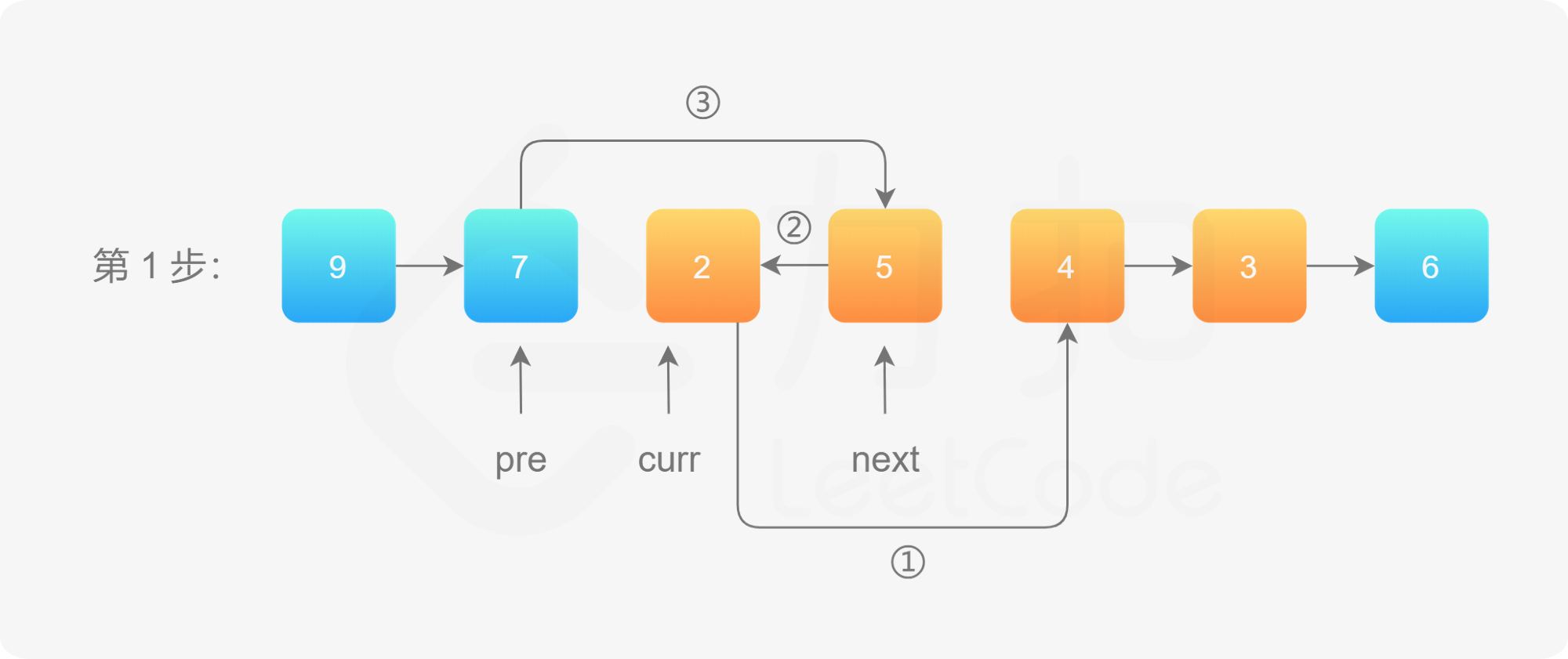
  • 头插法（需要记忆），代码比较难写
    • 先将 curr 的下一个节点记录为 next；
    • 执行操作 ①：把 curr 的下一个节点指向 next 的下一个节点；
    • 执行操作 ②：把 next 的下一个节点指向 pre 的下一个节点；
    • 执行操作 ③：把 pre 的下一个节点指向 next。

image.png

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        ListNode pre = dummy;
        for(int i = 0; i<left-1; i++){
            pre = pre.next;
        }
        ListNode cur = pre.next;
        ListNode nxt;
        //头插法
        for(int i = 0;i<right-left;i++){
            nxt = cur.next;
            cur.next = nxt.next;
            nxt.next = pre.next;
            pre.next= nxt;

        }
        return dummy.next;
    }
}
  • 递归反转

先实现反转前N，再将头指针调整至要反转的起始节点

class Solution {
    ListNode pre;
    public ListNode reverseBetween(ListNode head, int left, int right) {
        while(left == 1){
            return reverseN(head,right);
        }

        head.next = reverseBetween(head.next,left-1,right-1);//将head指针调整到left位置，并用reverseN函数
        return head;
    }

    private ListNode reverseN(ListNode head, int n){
        if(n==1){
            pre = head.next;
            return head;
        }
        ListNode last = reverseN(head.next,n-1);
        head.next.next = head;
        head.next = pre;
        return last;
    }
}

反转一组

25. K 个一组翻转链表

题目：

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

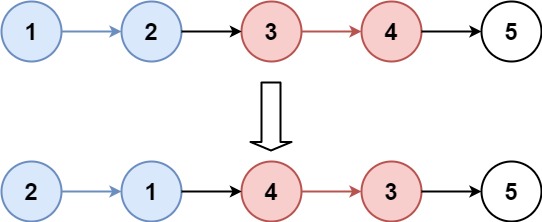
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

img

思路：

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null) return null;
        // 区间 [a, b) 包含 k 个待反转元素
        ListNode a, b;
        a = b = head;
        for(int i = 0;i<k;i++){
            if(b==null){
                return head;
            }
            b = b.next;//调整到下一个head
        }

	      //注意这个地方
        ListNode newHead = reverse(a,b);
        a.next = reverseKGroup(b,k);
        return newHead;
    }
    ListNode reverse(ListNode a, ListNode b) {
        ListNode pre, cur, nxt;
        pre = null; cur = a; nxt = a;
        // while 终止的条件改一下就行了
        while (cur != b) {
            nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        // 返回反转后的头结点
        return pre;
    }
}

滑动窗口

思路：

看到用滑动窗口的题，直接套模版

public void resolve(){
  Map<Character,Integer> window = new HashMap<>();//window，窗口内元素出现的次数。<元素，出现次数>
  Map<Character,Integer> need = new HashMap<>();//need，标准元素出现的次数
  int l = 0;
  int r = 0;
  while(r还可以继续往右滑){
    r++;
    //操作
    //判断
    while(窗口需要收缩){
      l++
      //操作
			//判断
    }
  }
}

简单的数组滑动窗口模版

function solution(nums, target) {
	let left = 0; //左边界
	let right = 0; //右边界
	let sum = 0;
	let res = Infinity;
	while (right < nums.length) {
		//还能往右滑
		sum += nums[right]; //右滑一个
		while (sum >= target) {
			//可以收缩窗口
			res = Math.min(res, right - left + 1);
			sum -= nums[left++];
		}
		right++; //右滑一个结束
	}
}

220. 存在重复元素 III

题目：

给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j，使得 abs(nums[i] - nums[j]) <= t ，同时又满足 abs(i - j) <= k 。如果存在则返回 true，不存在返回 false。

输入：nums = [1,2,3,1], k = 3, t = 0
输出：true

思路：

看到题目，要找一个区间内 下标之差<=k是否存在两个数值之差<=t的元素。很容易想到使用滑动窗口。

现在需要寻找一种数据结构，满足以下条件：

  • 支持添加删除元素，便于维护滑动窗口
  • 内部元素有序
  • 易于查找，能够查找到是否存在某个区间内的数字。

Java中，底层使用红黑树实现的TreeSet能够解决我们的问题。

查找某个区间内的元素，可以使用这个方法:

比如现在窗口内新增一个元素u，我想要知道是否存在一个元素与u的差值是否小于等于 t 那么我只需要知道是否存在一个元素落在区间 [u-t,u+t]中 进一步，我只需要找到所有 >=u-t的最小元素，是否 <=u+t即可。

而找这种边界数字，TreeSet刚好可以实现

代码:

class Solution {
    public boolean containsNearbyAlmostDuplicate(int[] nums, int indexDiff, int valueDiff) {
        TreeSet<Long> window = new TreeSet<Long>();
        int r = 0;
        int l = 0;
        while(r<nums.length){
            Long ceil = window.ceiling((long)(nums[r]-valueDiff)); //找>=nums[r]-valueDiff的最小元素
            if(ceil != null && ceil<=(long)(nums[r]+valueDiff)){//看这个元素是否<=nums[r]+valueDiff
                return true;
            }
            window.add((long)nums[r]);//这句不能放在上面，如果不存在，窗口扩大
            r++;
            if(r-l>indexDiff){
                //窗口大小超过了indexDiff，需要缩小窗口
                window.remove((long)nums[l]);
                l++;
            }
        }
        return false;
    }
}

滑动哈希

187. 重复的DNA序列

题目：

DNA序列 由一系列核苷酸组成，缩写为 ‘A’, ‘C’, ‘G’ 和 ‘T’.。例如，“ACGAATTCCG” 是一个 DNA序列 。在研究 DNA 时，识别 DNA 中的重复序列非常有用。给定一个表示 DNA序列 的字符串 s ，返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。

输入：s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
输出：["AAAAACCCCC","CCCCCAAAAA"]

思路：

滑动窗口+hash

前缀和

560. 和为 K 的子数组【基础】

题目：

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

输入：nums = [1,1,1], k = 2
输出：2
525. 连续数组
523. 连续的子数组和
327. 区间和的个数
918. 环形子数组的最大和

和环形dp一样，把子数组拆分成两部分考虑

974. 和可被 K 整除的子数组

难度中等434

// 注意 Java 取模的特殊性，当被除数为负数时取模结果为负数，需要纠正

1171. 从链表中删去总和值为零的连续节点

  • 题目：

    给你一个链表的头节点 head，请你编写代码，反复删去链表中由 总和 值为 0 的连续节点组成的序列，直到不存在这样的序列为止。

    删除完毕后，请你返回最终结果链表的头节点。

  • 思路：

    /**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeZeroSumSublists(ListNode head) {
        ListNode dummy = new ListNode(0,head);
        int presum = 0;
        HashMap<Integer,ListNode> map = new HashMap<>();
        for(ListNode node = dummy; node!=null;node= node.next){
            presum+=node.val;
            map.put(presum,node);
        }
        presum = 0;
        for(ListNode node = dummy; node!=null; node= node.next){
            presum+=node.val;
            if(map.containsKey(presum)){
                node.next = map.get(presum).next;
            }
        }
        return dummy.next;
    }
}

  • 注意，链表的头节点需要修改时，要使用虚拟节点 dummy

差分数组

差分数组 / 贪心

1094. 拼车-

题目：

车上最初有 capacity 个空座位。车 只能 向一个方向行驶（也就是说，不允许掉头或改变方向。给定整数 capacity 和一个数组 trips ,  trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客，接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

输入：trips = [[2,1,5],[3,3,7]], capacity = 4
输出：false

思路：

  • 差分数组【经典解法】

    经典解法，用差分数组，乘客在起始点上车和在终点下车，可以模拟为：对一个数组的一个区间进行加操作。得到差分数组后，可以反推出每个地点的乘客数量，如果有某个点乘客数量大于 容量，那么就返回 false。

    这里需要注意的是，由于我们不知道有多少个点，因此需要从数据范围中寻找 diff数组需要开辟的空间。

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
        int[] diff = new int[1001];
        int m = trips.length;
        for(int i = 0;i<m;i++){
            diff[ ] += trips[i][0];
            if(trips[i][2] < 1001){
                diff[trips[i][2]] -= trips[i][0];
            }
        }

        int[] res = new int[1001];
        res[0] = diff[0];
        if(res[0] >capacity){
            return false;
        }
        for(int i = 1;i<1001;i++){
            res[i] = res[i-1]+ diff[i];
            if(res[i] > capacity){
                return false;
            }
        }
        return true;
    }
}

  • 优先级队列+构造新类+贪心

    这个解法比较新，记录。

    首先，将 trips数组按照开始站点从小到大排序。接着，创建一个优先级队列（小根堆），维护 trips数组每个 trip的结束站点。然后，遍历 trips。

    如果当前的 trip的开始站点，大于等于优先级队列中的队首结束站点，那么就应该调整优先级队列，因为队首的那个 trip的乘客已经全部下车了

while(!pq.isEmpty() && pq.peek().end <= trip.start){
  Trip t = pq.poll();
  sum -= t.cnt;
}

如果当前的`trip`的开始站点，小于优先级队列中的队首结束站点，那么当前 `trip`入队。

最后，更新当前车上的乘客数，并判断是否大于`capacity`

由于优先级队列需要根据`trip`的结束时间排序，需要获取队首元素的结束站点，上车人数。因此需要建一个辅助类 `Trip`，将每一个 `trip`存成这个辅助类，加入优先级队列中。

完整代码如下 ：

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
        Arrays.sort(trips,(int[] a,int[] b) -> a[1] - b[1]);
        int m = trips.length;
        PriorityQueue<Trip> pq = new PriorityQueue<Trip>((Trip a,Trip b)-> a.end-b.end);
        pq.offer(new Trip(trips[0][0],trips[0][1],trips[0][2])); //结束时间
        int sum = trips[0][0];
        if(sum>capacity){
            return false;
        }
        for(int i = 1 ; i<m ; i++){
            Trip trip = new Trip(trips[i][0],trips[i][1],trips[i][2]);
            //这里要包含等于的情况，因为上车和下车同时发生时，也要调整队列。
            if(trip.start >= pq.peek().end){
                while(!pq.isEmpty() && pq.peek().end <= trip.start){
                    Trip t = pq.poll();
                    sum -= t.cnt;
                }
                pq.offer(trip);
                sum += trip.cnt;
            }else{
                pq.offer(trip);
                sum += trip.cnt;
            }
            if(sum>capacity){
                return false;
            }
        }
        return true;
    }
}
class Trip{
    int start;
    int end;
    int cnt;
    Trip( int cnt, int start, int end){
        this.start = start;
        this.end = end;
        this.cnt = cnt;
    }
}

模拟

找到循环的规律

54. 螺旋矩阵

54. 螺旋矩阵

单调栈

用处：通常需要找左边/右边第一个比自己大/比自己小的元素就会用到单调栈。

思路：如果要找右边第一个比自己大的元素，就维护一个递增的栈。

var dailyTemperatures = function (temperatures) {
	const stack = new Array();
	const res = Array.from({ length: temperatures.length });
	stack.push(0);
	for (let i = 1; i < temperatures.length; i++) {
		while (temperatures[stack[stack.length - 1]] < temperatures[i] && stack.length > 0) {
			const top = stack.pop();
			res[top] = i - top;
		}
		stack.push(i);
	}
	stack.forEach((s) => {
		res[s] = 0;
	});
	return res;
};